Математика

Аналитическая теория чисел

В аналитической теории чисел для вывода и доказательства утверждений о числах и числовых функциях используется мощный аппарат математического анализа. Первым шагом в этом направлении стал метод производящих функций, сформулированный Эйлером. Для определения количества целочисленных неотрицательных решений линейного уравнения вида
a_1 x_1+...+a_n x_n=N, где a_1,...,a_n — натуральные числа,
Эйлер построил производяшую функцию, которая определяется как произведение сходящихся рядов (при |z|<1) F_i(z)=\sum^\infty_{k=0}{z^a_i k} и является суммой членов геометрической прогрессии, при этом
F(z)=\sum^\infty_{N=0}l(N) z^N, где l(N) — число решений изучаемого уравнения.
На основе этого метода был построен круговой метод Харди — Литлвуда[2].
В работе над квадратичным законом взаимности Гаусс рассмотрел конечные суммы вида S(a)=\sum^{p}_{n=1} e^{2\pi i an^2/p}, которые могут быть представлены в виде суммы синусов и косинусов (по формуле Эйлера), из-за чего они являются частным случаем тригонометрических сумм[2]. Метод тригонометрических сумм, позволяющий оценивать число решений тех или иных уравнений или систем уравнений в целых числах играет большую роль в аналитической теории чисел. Основы метода разработал и впервые применил к задачам теории чисел И. М. Виноградов.
Работая над доказательством теоремы Евклида о бесконечности простых чисел Эйлер рассмотрел произведение по всем простым числам и сформулировал тождество:
\Pi_p \left ( 1-\frac{1}{p_s} \right ) ^{-1}=\sum^\infty_{n=1} \frac{1}{n^s},
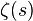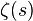которое стало основанием для теорий дзета-функций[2]. Наиболее известной и до сих пор не решённой проблемой аналитической теории чисел является доказательство гипотезы Римана о нулях дзета-функции, утверждающей, что все нетривиальные корни уравнения \zeta(s) = 0 лежат на так называемой критической прямой \mathrm{Re}\,s = \frac{1}{2}, где \zeta(s) — дзета-функция Римана.
Для доказательства теоремы о бесконечности простых чисел в общем виде Дирихле использовал произведения по всем простым числам, аналогичные эйлерову произведению, и показал, что
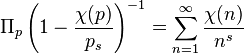\Pi_p \left (1-\frac{\chi (p)}{p_s} \right )^{-1}=\sum^\infty_{n=1} \frac{\chi (n)}{n^s},
при этом функция \chi(p), получившая название характер Дирихле, определена так, что удовлетворяет следующим условиям: она является периодической, вполне мультипликативной и не равна тождественно нулю. Характеры и ряды Дирихле нашли применение и в других разделах математики, в частности в алгебре, топологии и теории функций[2].
Чебышев показал, что число простых чисел, не превосходяших X, обозначенное как \pi (X), стремится к бесконечности по следующему закону:
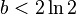a \frac{X}{\ln(X)} < \pi(X) < b \frac{X}{\ln(X)}, где a>1/2 \ln 2 и b<2 \ln 2[2].
Другим направлением аналитической теории чисел является применение комплексного анализа в доказательстве теоремы о распределении простых чисел.

Комментариев нет:

Отправить комментарий

Подписаться на: Сообщения (Atom)